Pipes & Cistern
Important Instructions
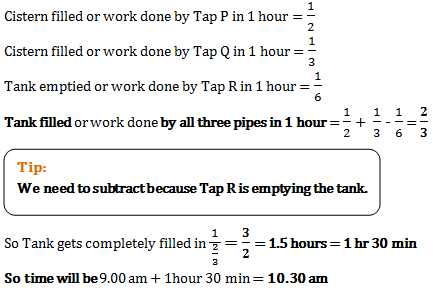
Tap P alone fills a cistern in 2 hours; while tap Q alone fills the same cistern in 3 hours. A new tap R is attached to the bottom of the cistern which can empty the completely filled cistern in 6 hours. Sunny started all three taps together at 9am. When will the tank be full?
Answer: A
Enter details here
A large tanker can be filled by two pipes A and B in 60 minutes and 40 minutes respectively. How many minutes will it take to fill the tanker from empty state if B is used for half the time and A and B fill it together for the other half?
Answer: D
| Part filled by (A + B) in 1 minute = |  |
1 | + | 1 |  |
= | 1 | . |
| 60 | 40 | 24 |
Suppose the tank is filled in x minutes.
| Then, | x | |
1 | + | 1 | |
= 1 |
| 2 | 24 | 40 |
 |
x | x | 1 | = 1 |
| 2 | 15 |
x = 30 min.
Enter details here
A inlet pipe can fill a tank in 12 hours and an outlet pipe can empty the tank in 16 hours. If both the pipes are opened simultaneously, find the time taken to fill the tank.
Answer: D
As the inlet can fill the tank in 12 hours, in one hour it will fill 1/12th of the tank.
Similarly, the outlet pipe in one hour can empty 1/16th part of the tank.
If both are opened simultaneously, the part of the tank filled in one hour is:
1/12 - 1/16 = 1/48
Hence, the tank gets filled in 48 hours.
Enter details here
If pipe A can fill the tank in 45 minutes and pipe B in 30 minutes, find the time to fill the tank if both the pipes are opened together.
Answer: C
In 1 minute pipe A can fill 1/45th part of the tank and pipe B can fill 1/30th part of the tank. If they are opened simultaneously then in 1 minute they can fill (1/45 + 1/30) part of the tank = 1/18th part of the tank.
Hence, in 18 minutes the tank gets filled if pipes A & B are opened together.
Enter details here
A cistern is normally filled with water in 10 hours but takes 5 hours longer to fill because of a leak in its bottom. If the cistern is full, the leak will empty the cistern in
Answer: D
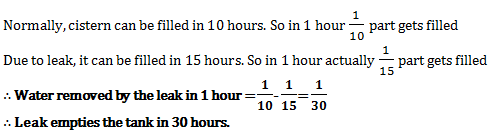
Enter details here
Two pipes A and B can fill a tank in 15 minutes and 20 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?
Answer: D
| Part filled in 4 minutes = 4 | |
1 | + | 1 | |
= | 7 | . |
| 15 | 20 | 15 |
| Remaining part = | |
1 - | 7 | |
= | 8 | . |
| 15 | 15 |
| Part filled by B in 1 minute = | 1 |
| 20 |
 |
1 | : | 8 | :: 1 : x |
| 20 | 15 |
| x = | |
8 | x 1 x 20 | |
= 10 | 2 | min = 10 min. 40 sec. |
| 15 | 3 |
The tank will be full in (4 min. + 10 min. + 40 sec.) = 14 min. 40 sec.
Enter details here
Two pipes A and B can fill a cistern in 37.5 minutes and 45 minutes respectively. This cistern will be filled in half an hour if both the pipes are opened together initially and pipe B is then turned off after X minutes. What is X?
Answer: D
Let B be turned off after X minutes.
Part of water will be filled by A + B in x minutes + After tap B is closed rest filled by A in (30-x) minutes = 1
=> x/(time taken to fill the container by each separately) + 30 - x/(time taken to fill the container by A alone) = 1
=> x(2/75 + 1/45) + (30-x)2/75 = 1
=> 11x + 180 – 6x = 225
Therefore, x = 9 minutes
Enter details here
Two pipes can fill a tank in 10 hours and 12 hours resp. while third pipe empties the full tank in 20 hours. If all the three pipes operate simultaneously, in how much time the tank will be filled?
Answer: A
Pipe A can fill a tank in x hours and pipe B can fill a tank in y hours and pipe C can empty it in z hours. If all the pipes are operate simultaneously, 1 hours of work of each of the three pipes = 1/x +1/y – 1/z
1 minutes work of each of the three pipes = 1/10 + 1/12 – 1/20 = 15/2 hours
= 7 ½ hour = 7 hours 30 minutes.
Enter details here
A large tanker can be filled by 2 pipes A and B in 60 minutes respectively. How many minutes will it take to fill the tanker from empty state if B is used for half the time and A &B fill it together for the other half time ..?
Answer: D
No answer description available for this question.
Enter details here
Two pipes A and B together can fill a cistern in 4 hours. Had they been opened separately, then B would have taken 6 hours more than A to fill the cistern. How much time will be taken by A to fill the cistern separately?
Answer: C
Let the cistern be filled by pipe A alone in x hours.
Then, pipe B will fill it in (x + 6) hours.
|
1 | + | 1 | = | 1 |
| x | (x + 6) | 4 |
|
x + 6 + x | = | 1 |
| x(x + 6) | 4 |
x2 - 2x - 24 = 0
(x -6)(x + 4) = 0
x = 6. [neglecting the negative value of x]
Enter details here
Topics
- Number System
- H.C.F. & L.C.M.
- Decimal Fractions
- Simplification
- Average
- Problems on Numbers
- Problems on Ages
- Percentage
- Profit & Loss
- Ratio & Proportion
- Time & Work
- Pipes & Cistern
- Time & Distance
- Problems on Trains
- Boats & Streams
- Simple Interest
- Compound Interest
- Area
- Volume & Surface Areas
- Mensuration
- Races & Games of Skill
- Clocks
- Permutations & Combinations
- Probability
- Odd Man Out & Series
- Algebra