Pipes & Cistern
Important Instructions
A tank is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the tank in the same time during which the tank is filled by the third pipe alone. The second pipe fills the tank 5 hours faster than the first pipe and 4 hours slower than the third pipe. The time required by the first pipe is:
Answer: C
Suppose, first pipe alone takes x hours to fill the tank .
Then, second and third pipes will take (x -5) and (x - 9) hours respectively to fill the tank.
 |
1 | + | 1 | = | 1 |
| x | (x - 5) | (x - 9) |
 |
x - 5 + x | = | 1 |
| x(x - 5) | (x - 9) |
 (2x - 5)(x - 9) = x(x - 5)
(2x - 5)(x - 9) = x(x - 5)
 x2 - 18x + 45 = 0
x2 - 18x + 45 = 0
(x - 15)(x - 3) = 0
 x = 15. [neglecting x = 3]
x = 15. [neglecting x = 3]
Enter details here
A tank is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the tank in the same time during which the tank is filled by the third pipe alone. The second pipe fills the tank 5 hours faster than the first pipe and 4 hours slower than the third pipe. Find the time required by the first pipe to fill the tank ?
Answer: B
Suppose, first pipe alone takes x hours to fill the tank .
Then, second and third pipes will take (x -5) and (x - 9) hours respectively to fill the tank.
As per question, we get
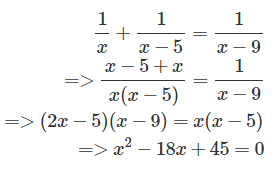
After solving this equation, we get
(x-15)(x+3) = 0,
As value can not be negative, so x = 15
Enter details here
A leak at the bottom of the tank can empty the tank in 5 hours, while an inlet pipe can fill the same tank at the rate of 6 litres per minute. When the tank is full, the inlet is opened and the tank gets empty in 8 hours due to the leakage. Find the capacity of the tank.
Answer: C
The capacity of the tank is given by C = (p*q*r)/(r – p) litres
Where, p = time in which the leakage can empty the tank in hours = 5 hours
q = rate at which the inlet fills the tank in lph = 6*60 = 360 lph
r = time in which the tank gets emptied in hours = 8 hours
Hence, C = (5*360*8)/(8 – 5)
C = 4800 litres
Enter details here
An electric pump fills a tank in 3 hours. Due to leakage in the tank, it took 3 hours 30 min to fill. In how much time will the leakage drain out all the water of the tank make it empty ?
Answer: D
We can get the answer by subtrating work done by leak in one hour by subtraction of filling for 1 hour without leak and with leak, as
Work done for 1 hour without leak = 1/3
Work done with leak =
3 1/2=7/2
Work done with leak in 1 hr = 2/7
Work done by leak in 1 hr = 1/3−2/7 = 1/21
So tank will be empty by the leak in 21 hours.
Enter details here
A cistern is filled by tap A in 4 hours where as it can be emptied by tap B in 9 hours. If both the taps are opened simultaneously, in how much time will the cistern be filled ?
Answer: C
When we have question like one is filling the tank and other is empting it, then we subtraction as,
Filled in 1 hour = 1/4
Empties in 1 hour = 1/9
Net filled in 1 hour = 1/4 - 1/9
= 5/36
So cistern will be filled in 36/5 hours i.e. 7.2 hours
Enter details here
If x + 5y = 16 and x= -3y, then y =
Answer: C
There is no explanation.
Enter details here
A tap can fill a tank in 48 minutes where as another tap can empty it in 2 hours. If both taps are opened at 11.40 AM, then the tank will be filled at .. ?
Answer: B
No answer description available for this question.
Enter details here
Pipes A and B can fill a tank in 5 and 6 hours respectively. Pipe C can empty it in 12 hours. If all the three pipes are opened together, then the tank will be filled in:
Answer: C
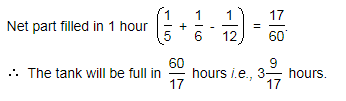
Enter details here
One pipe can fill a tank three times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in
Answer: A
Let the slower pipe alone fill the tank in x minutes
then faster will fill in x/3 minutes.
Part filled by slower pipe in 1 minute = 1/x
Part filled by faster pipe in 1 minute = 3/x
Part filled by both in 1 minute =
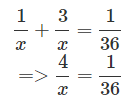
x = 36 × 4 = 144 mins
Enter details here
A tank is by pipe A in 5 hours, pipe B in 10 hours and pipe C 30 hours. How much time will all the pipes together take to fill the tank?
Answer: D
Part filled by A in 1 hour = 1/5
Part filled by B in 1 hour = 1/10
Part filled by C in 1 hour = 1/30
Part filled by (A+B+C) in 1 hour =
1/5+1/10+1/30
=1/3
So all pipes will fill the tank in 3 hours.
Enter details here
Topics
- Number System
- H.C.F. & L.C.M.
- Decimal Fractions
- Simplification
- Average
- Problems on Numbers
- Problems on Ages
- Percentage
- Profit & Loss
- Ratio & Proportion
- Time & Work
- Pipes & Cistern
- Time & Distance
- Problems on Trains
- Boats & Streams
- Simple Interest
- Compound Interest
- Area
- Volume & Surface Areas
- Mensuration
- Races & Games of Skill
- Clocks
- Permutations & Combinations
- Probability
- Odd Man Out & Series
- Algebra